Dérivée de racine de x. Toutes les versions de cet article : < English > <français> < italiano >. La dérivée f’ de la fonction racine carré de x f (x)=√x est pour.
🎁 Comment Booster Tes Notes dès le prochain DS ? Suis ce lien, c’est cadeau : https://www.lesmathsentongs.com/ebook⬇︎ ⬇︎ ⬇︎ ⬇︎ ⬇︎ ⬇︎💎 ...
http://jaicompris.com/lycee/math/fonction/derivation/derivation-calcul.phpObjectifs:- savoir démontrer la formule de dérivation: f(x)=√x alors f'(x)=1/(2√x)-...
Le résolveur gratuit de problèmes de maths répond à vos questions d’algèbre, de géométrie, de trigonométrie, de calcul et de statistiques avec des explications détaillées, tout.
Calculateurs gratuit de pré-algèbre, algèbre, trigonométrie, calculs, géométrie, statistiques et chimie, étape par étape Solutions Graphisme ... (tan^{-1}\left(x\right)\right) fr..
Pour le calcul en ligne la dérivée d'une fonction composée, il suffit de saisir l'expression mathématique qui contient la fonction composée, de préciser la variable et d'appliquer la.
Dérivée de 1/x. dimanche 10 janvier 2021, par Nadir Soualem. 1/x dérivée fonction. Toutes les versions de cet article : < English > <français> < italiano >. La.
+14 Derivee De 1 Racine X Ideas. < english > <français> la dérivée f’ de la fonction f. Tu vois que pour te rappeler de la dérivée de la racine de x, il suffit de te.
Comme −1 - 1 est constant par rapport à x x, la dérivée de −x2 - x 2 par rapport à x x est − d dx [x2] - d d x [ x 2]. 1 2(1− x2)1 2 (− d dx [x2]) 1 2 ( 1 - x 2) 1 2 ( - d d x [ x 2]).
1/racine (x) est localement intégrable. Elle définit donc une distribution. Elle est donc dérivable. Question : quelle est sa dérivée ? Après quelques calculs, je suis.
Nous pouvons voir un exemple du théorème des valeurs extrêmes en action sur cette figure ; le minimum global de notre fonction sur cet intervalle est au point 𝑥 = − 1 où la fonction.
Calculatrice en ligne - deriver (racine_cubique (x)) - Solumaths. Le calculateur de dérivée permet le calcul de la derivée d'une fonction par rapport à une variable avec le détail et.
Dérivée de la somme (u+v)0= u0+v0 Dérivée du produit par un scalaire (ku)0= ku0 Dérivée du produit (uv)0= u 0v+uv Dérivée de l’inverse 1 u! 0 = u0 u2 Dérivée du.

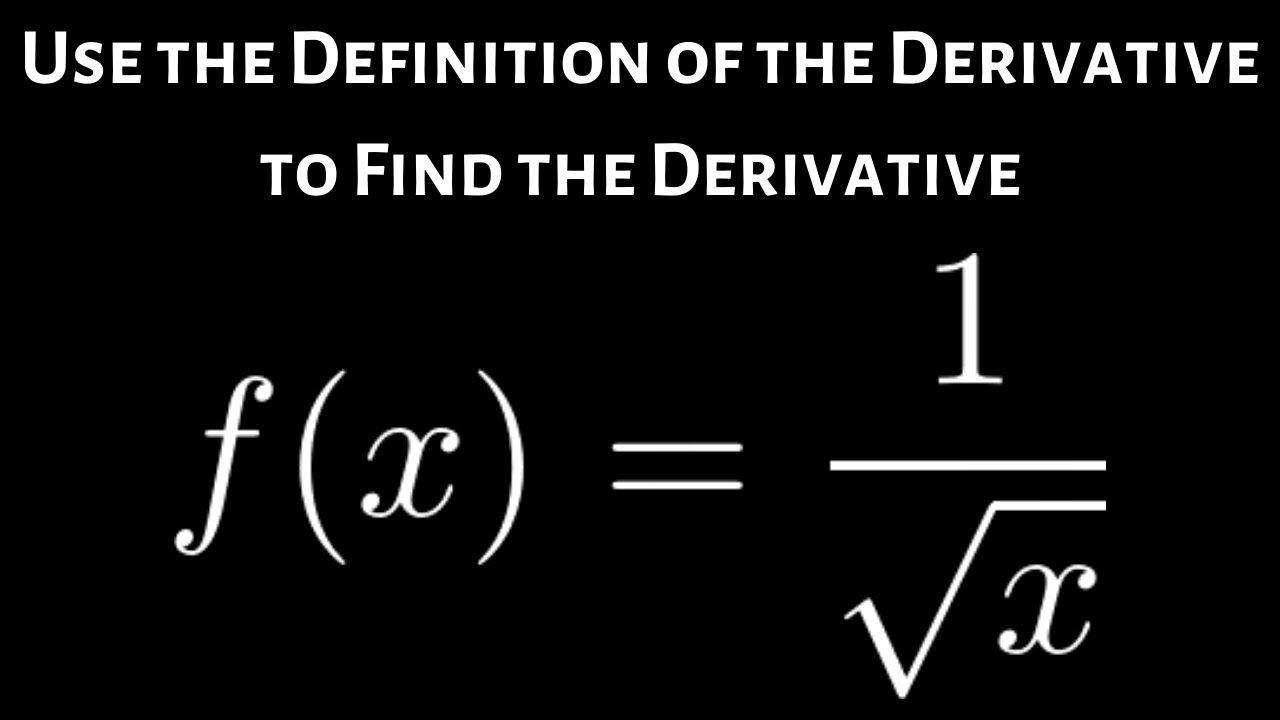



![Derivee De 1 Racine De X CALCUL DE PRIMITIVE D'UNE FONCTION Contenant une Racine Carrée - 2 BAC - [EXERCICE 2] - YouTube](https://i.ytimg.com/vi/SW2RdjrnRTc/maxresdefault.jpg)








